文章內容目錄
三點求圓方程推導
假設有一個圓,圓心坐標為 (x0, y0),半徑為 r。則圓的方程可表示為:
(x – x0)^2 + (y – y0)^2 = r^2
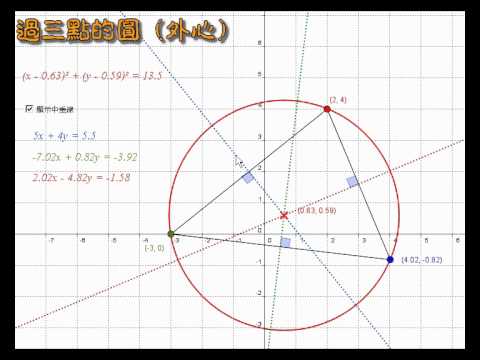

給定圓上三個點 (x1, y1),(x2, y2) 和 (x3, y3),可列出以下等式:
(x1 – x0)^2 + (y1 – y0)^2 = r^2
(x2 – x0)^2 + (y2 – y0)^2 = r^2
(x3 – x0)^2 + (y3 – y0)^2 = r^2
將第一個和第二個等式相減,再將第一個和第三個等式相減,化簡後得到:

2(x1 – x2) * (x0 – 0.5(x1 + x2)) + 2(x2 – x3) * (x0 – 0.5(x2 + x3)) = 0
2(y1 – y2) * (y0 – 0.5(y1 + y2)) + 2(y2 – y3) * (y0 – 0.5(y2 + y3)) = 0
若係數矩陣的行列式不為 0,則圓心 (x0, y0) 存在唯一解:
| | (x1 - x2) (x1 - x3) | | |
| | (y1 - y2) (y1 - y3) | | |
| |-2(x1 - x2*0.5*(x1 + x2))-2(x2 - x3*0.5*(x2 + x3)) | |=0
| |-2(y1 - y2*0.5*(y1 + y2))-2(y2 - y3*0.5*(y2 + y3)) | |
圓心 (x0, y0) 解出後,將任意一個給定點代回圓方程即可求得半徑 r:
r^2 = (xi – x0)^2 + (yi – y0)^2
最終得到的圓方程為:
三點成圓:幾何學中的基礎原理
在幾何學中,「三點成圓」是一個基本原理,説明給定任何三點,都能找到一個圓通過這三點。這個原理廣泛應用於幾何學和工程學領域。
三點成圓的證明
考慮三點 A、B、C,不妨將其坐標設為 (x₁, y₁)、(x₂, y₂) 和 (x₃, y₃)。假設圓心為 (h, k),其半徑為 r。根據圓的定義,三點到圓心的距離相等:
|A - (h, k)| = |B - (h, k)| = |C - (h, k)| = r
將上述等式帶入距離公式,可得:
(h - x₁)² + (k - y₁)² = r²
(h - x₂)² + (k - y₂)² = r²
(h - x₃)² + (k - y₃)² = r²
減掉後兩式中的第一式,消去 r²,可得:
2(x₁ - x₂)h + 2(y₁ - y₂)k - x₁² - y₁² = 2(x₂ - x₃)h + 2(y₂ - y₃)k - x₂² - y₂²
展開並整理,可得:
(x₁² + y₁² - x₂² - y₂²)h + (x₂² + y₂² - x₃² - y₃²)k = (x₂y₁ - x₁y₂) + (x₃y₂ - x₂y₃)
這是一個關於 h 和 k 的一元一次方程組。求解方程組可得到圓心的坐標:
h = {((x₂ - x₃)(y₁ - y₂) - (x₁ - x₂)(y₂ - y₃))/(2(x₁y₂ - x₂y₁ + x₃y₁ - x₁y₃))}
k = {((x₃ - x₁)(y₂ - y₁) - (x₂ - x₃)(y₁ - y₂))/(2(x₁y₂ - x₂y₁ + x₃y₁ - x₁y₃))}
代入圓心坐標,即可得到圓的方程式:
(x - h)² + (y - k)² = r²
其中 r² 可由上述三點到圓心距離等式的任意一個求得。
三點成圓的應用
三點成圓原理在幾何學和工程學中廣泛應用,例如:
延伸閲讀…
三點確定一個圓的計算方法原創
三點求圓方程
- 圓心定位:給定圓上的三點,可以利用三點成圓原理求出圓心。
- 圓周長和麪積計算:知道圓心和半徑後,可以計算圓周長和麪積。
- 圓弧長度計算:給定圓的圓心、半徑和端點,可以計算圓弧長度。
- 圓錐和球體體積計算:圓錐和球體都是以圓為基礎的立體圖形。通過利用三點成圓原理確定圓的參數,可以計算圓錐或球體的體積。
表格:三點成圓原理的應用
| 應用 | 步驟 |
|---|---|
| 圓心定位 | 解決上述一元一次方程組,求出圓心坐標。 |
| 圓周長計算 | 根據圓心和半徑,計算圓周長。 |
| 圓面積計算 | 根據圓心和半徑,計算圓面積。 |
| 圓弧長度計算 | 根據圓心、半徑和端點,計算圓弧長度。 |
| 圓錐體積計算(底面為圓) | 確定圓底面的圓心和半徑,然後使用圓錐體積公式計算體積。 |
| 球體體積計算 | 確定球體表面上的三點,根據三點成圓原理求出球心和半徑,然後使用球體體積公式計算體積。 |

